You might be wondering, what do all three items in the title have in common? They are a product of my first week in graduate school! Let me explain. I am currently enrolled in two courses: measure theory and abstract algebra. My first week of measure theory was kind of confusing. We started in chapter 6 of Real Analysis by H. Royden with the goal of proving Lebesgue’s Differentiation Theorem. This powerful statement says that a monotone function is differentiable almost everywhere. In order to get at this theorem, we first proved a lemma named the rising sun/sunrise lemma. This intuitive fact, brought to us by Riesz, says suppose
is continuous. Let
. Then
is open, so
and
for all
in some indexing set
. The picture describing this is
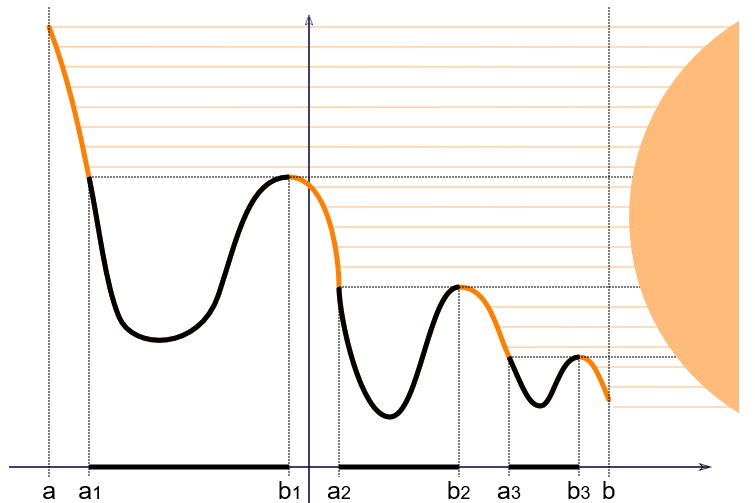
The set that we are concerned with in the lemma is precisely the shadows being cast by the sun in the picture. Surprisingly, the proof of this (seemingly intuitive fact) took nearly two class periods. This was a super cool proof, and I recommend any reader to dive deeper into the mechanics of the statement!
My abstract algebra course has been flying by. We covered nearly all of chapter 0 and 1 of Dummit & Foote in the first 3 meetings. Luckily, much of these chapters contains material that should be review. We have not proven any serious results in the class yet, but we are well on our way to doing just that. This class has shown me that graduate school moves fast. We are covering a lot of material in a very short amount of time. The onus of learning has blatantly shifted from teacher to student. I am looking forward to learning new material, but I also know that it will be taxing when said new material is encountered. The sailing has been smooth thus far, but I see choppy waters on the horizon.
I have also held my first recitation! I was pretty nervous to stand in front of a class of 30+ as an authority figure, but I think that my two sections turned out well. I am given a lot of freedom in how to supplement their learning in these meetings, and I employed two different techniques in my back to back sections. My first section broke off into groups of 5-7 to work on relevant problems to help study for their first quiz. I was able to walk around and answer questions as students needed. The stronger students were often able to help their acquaintances while strengthening their own foundations. In my second section, I employed a more lecture focused style. I stood at the board and walked the whole class through difficult problems that would help prepare them for their quiz. One observation I have is that the students were much more receptive to this approach and were happy to see me working out problems for them. However, I think that the first strategy forced the students to engage their minds and work as a team to gain success.
Overall, my first week has been exceptionally busy. I have been dreaming of math and my office nearly every night, but I do not consider these nightmares. People often say that doing what you love for a living has a tendency to turn you off to the activity, but I am happier than ever. I am able to think about math all day, and I know that I made the right choice by pursuing this lifestyle.
Feel free to email me at mitch.haeuser42@gmail.com if you have any questions regarding content, my graduate school experience, or anything else!